Chapter 4: Control-Based Algorithms
This chapter describes the dominant congestion-control algorithm in use today on the Internet. The approach was introduced in 1988 by Van Jacobson and Mike Karels, and refined multiple times over the years. The variant in widespread use today is called CUBIC, for reasons that will become clear at the end of the chapter.
The general idea is straightforward. Having transmitted a set of packets according to its current estimate of the available bandwidth, a TCP sender reacts to two signals from the network. On the one hand, the arrival of an ACK signals that one of its packets has left the network and that it is therefore safe to transmit a new packet without adding to the level of congestion. By using ACKs to pace the transmission of packets, TCP is said to be self-clocking. On the other hand, a timeout signals that a packet was lost, implying that the network is congested, and thus TCP needs to reduce its sending rate. Because using packet loss as a signal means congestion has already occurred and we are reacting after the fact, we refer to this approach as control-based.
There are many subtle issues that must be addressed to make this a practical approach to congestion control. This chapter describes the collection of techniques that address these issues, and as such, can be read as a case study of the experience of identifying and solving a sequence of problems. We will trace the historical context as we visit each of the techniques in the sections that follow.
4.1 Timeout Calculation
Timeouts and retransmissions are a central part TCP’s approach to implementing a reliable byte-stream, but timeouts also play a key role in congestion control because they signal packet loss, which in turn indicates the likelihood of congestion. In other words, TCP’s timeout mechanism is a building block for its overall approach to congestion control.
Note that a timeout can happen because a packet was lost, or because the corresponding acknowledgment was lost, or because nothing was lost but the ACK took longer to arrive than we were expecting. Hence it is important to know how long it might take an ACK to arrive, because otherwise we risk responding as if there was congestion when there was not.
TCP has an adaptive approach to setting a timeout, computed as a function of the measured RTT. As simple as this sounds, the full implementation is more involved than you might expect, and has been through multiple refinements over the years. This section revisits that experience.
4.1.1 Original Algorithm
We begin with the simple algorithm that was originally described in
the TCP specification. The idea is to keep a running average of the
RTT and then to compute the timeout as a function of this RTT.
Specifically, every time TCP sends a data segment, it records the
time. When an ACK for that segment arrives, TCP reads the time again,
and then takes the difference between these two times as a
SampleRTT. TCP then computes an EstimatedRTT as a weighted
average between the previous estimate and this new sample. That is,
The parameter \(\alpha\) is selected to smooth the
EstimatedRTT. A small \(\alpha\) tracks changes in the RTT but is
perhaps too heavily influenced by temporary fluctuations. On the other
hand, a large \(\alpha\) is more stable but perhaps not quick enough to
adapt to real changes. The original TCP specification recommended a
setting of \(\alpha\) between 0.8 and 0.9. TCP then uses
EstimatedRTT to compute the timeout in a rather conservative way:
4.1.2 Karn/Partridge Algorithm
After several years, a rather obvious flaw was discovered in this simple approach: An ACK does not really acknowledge a transmission, but rather, it acknowledges the receipt of data. In other words, whenever a segment is retransmitted and then an ACK arrives at the sender, it is impossible to determine if this ACK should be associated with the first or the second transmission of the segment for the purpose of measuring the sample RTT.
It is necessary to know which transmission to associate it with so as
to compute an accurate SampleRTT. As illustrated in
Figure 21, if you assume that the ACK is for
the original transmission but it was really for the second, then the
SampleRTT is too large (a); if you assume that the ACK is for the
second transmission but it was actually for the first, then the
SampleRTT is too small (b).
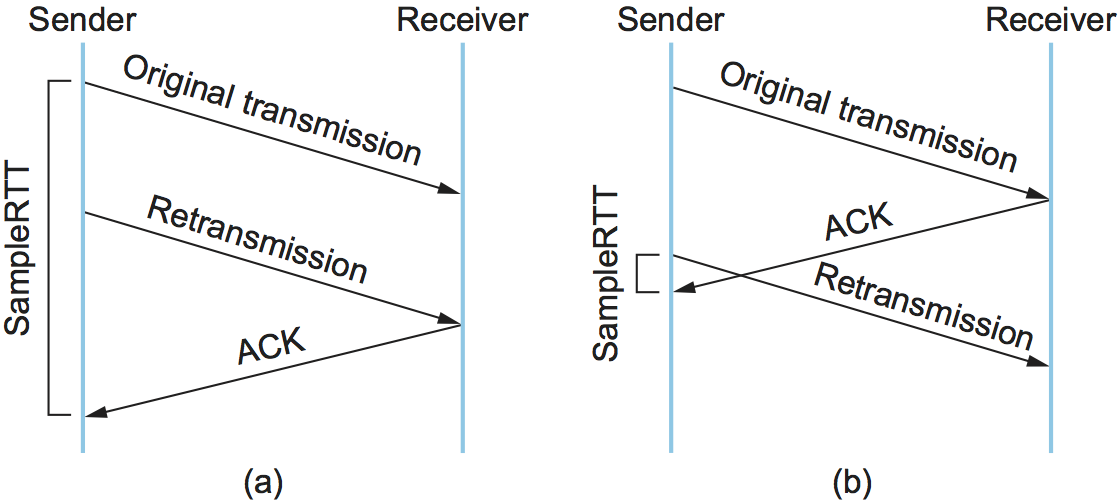
Figure 21. Associating the ACK with (a) original transmission versus (b) retransmission.
The solution at first looks surprisingly simple. It is known as the
Karn/Partridge algorithm, after its inventors. With this algorithm,
whenever TCP retransmits a segment, it stops taking samples of the
RTT; it only measures SampleRTT for segments that have been sent
only once. But the algorithm also includes a second change to TCP’s
timeout mechanism. Each time TCP retransmits, it sets the next timeout
to be twice the last timeout, rather than basing it on the last
EstimatedRTT. That is, Karn and Partridge proposed that timeout
calculation use exponential backoff. The motivation for using
exponential backoff is that timeouts cause retransmission, and
retransmitted segments are no longer contributing to an update in the
RTT estimate. So the idea is to be more cautious in declaring that a
packet has been lost, rather than getting into a possible cycle of
aggressively timing out and then retransmitting. We will see this
idea of exponential backoff again, embodied in a much
more sophisticated mechanism, in a later section.
4.1.3 Jacobson/Karels Algorithm
The Karn/Partridge algorithm was an improvement to RTT estimation, but it did not eliminate congestion. The 1988 congestion-control mechanism proposed by Jacobson and Karels includes (along with several other components) a new way to decide when to time out and retransmit a segment.
The main problem with the original computation is that it does not
take the variance of the sample RTTs into account. Intuitively, if the
variation among samples is small, then the EstimatedRTT can be
better trusted and there is no reason for multiplying this estimate by
2 to compute the timeout. On the other hand, a large variance in the
samples suggests that the timeout value should not be too tightly
coupled to the EstimatedRTT.
In the new approach, the sender measures a new SampleRTT as before.
It then folds this new sample into the timeout calculation as follows:
where \(\delta\) is between 0 and 1. That is, we calculate both
the weighted moving average of the RTT and the weighted moving average of its
variation. TCP then computes the
timeout value as a function of both EstimatedRTT and Deviation
as follows:
where based on experience, \(\mu\) is typically set to 1 and \(\phi\) is
set to 4. Thus, when the variance is small, TimeOut is close to
EstimatedRTT; a large variance causes the Deviation term to
dominate the calculation.
4.1.4 Implementation
There are two items of note regarding the implementation of timeouts
in TCP. The first is that it is possible to implement the calculation
for EstimatedRTT and Deviation without using floating-point
arithmetic. Instead, the whole calculation is scaled by 2n,
with \(\delta\) selected to be 1/2n. This allows us to do
integer arithmetic, implementing multiplication and division using
shifts, thereby achieving higher performance. The resulting
calculation is given by the following code fragment, where n=3 (i.e.,
\(\delta\) = 1/8). Note that EstimatedRTT and Deviation are
stored in their scaled-up forms, while the value of SampleRTT at
the start of the code and of TimeOut at the end are real, unscaled
values. If you find the code hard to follow, you might want to try
plugging some real numbers into it and verifying that it gives the
same results as the equations above.
{
SampleRTT -= (EstimatedRTT >> 3);
EstimatedRTT += SampleRTT;
if (SampleRTT < 0)
SampleRTT = -SampleRTT;
SampleRTT -= (Deviation >> 3);
Deviation += SampleRTT;
TimeOut = (EstimatedRTT >> 3) + (Deviation >> 1);
}
The second is that the algorithm is only as good as the clock used to read the current time. On typical Unix implementations at the time, the clock granularity was as large as 500 ms, which is significantly larger than the average cross-country RTT of somewhere between 100 and 200 ms. To make matters worse, the Unix implementation of TCP only checked to see if a timeout should happen every time this 500-ms clock ticked and would only take a sample of the round-trip time once per RTT. The combination of these two factors could mean that a timeout would happen 1 second after the segment was transmitted. An extension to TCP, described in the next section, makes this RTT calculation a bit more precise.
For additional details about the implementation of timeouts in TCP, we refer the reader to the authoritative RFC:
Further Reading
RFC 6298: Computing TCP’s Retransmission Timer. June 2011.
4.1.5 TCP Timestamp Extension
The changes to TCP described up to this point have been adjustments to
how the sender computes timeouts, with no changes to the over-the-wire
protocol. But there are also extensions to the TCP header that help
improve its ability to manage timeouts and retransmissions. We discuss
one that relates to RTT estimation here. Another extension, establishing a scaling factor for
AdvertisedWindow, was described in Section 2.3., and a third,
selective acknowledgment or SACK is discussed below.
The TCP timestamp extension helps to improve TCP’s timeout mechanism. Instead of measuring the RTT using a coarse-grained event, TCP can read the actual system clock when it is about to send a segment, and put this time—think of it as a 32-bit timestamp—in the segment’s header. The receiver then echoes this timestamp back to the sender in its acknowledgment, and the sender subtracts this timestamp from the current time to measure the RTT. In essence, the timestamp option provides a convenient place for TCP to store the record of when a segment was transmitted; it stores the time in the segment itself. Note that the endpoints in the connection do not need synchronized clocks, since the timestamp is written and read at the same end of the connection. This improves the measurement of RTT and hence reduces the risk of incorrect timeouts due to poor RTT estimates.
This timestamp extension serves a second purpose, in that it also
provides a way to create a 64-bit sequence number field, addressing
the shortcomings of TCP’s 32-bit sequence number outlined in Section 2.3.
Specifically, TCP decides whether to accept or reject a segment based
on a logical 64-bit identifier that has the SequenceNum field in
the low-order 32 bits and the timestamp in the high-order 32 bits.
Since the timestamp is always increasing, it serves to distinguish
between two different incarnations of the same sequence number. Note
that the timestamp is being used in this setting only to protect
against wraparound; it is not treated as part of the sequence number
for the purpose of ordering or acknowledging data.
4.2 Additive Increase/Multiplicative Decrease
A better way to compute timeouts is a necessary building block, but it
does not get at the heart of controlling congestion. The central
challenge is computing an estimate of how much traffic
this sender can safely transmit. To this end, TCP maintains a new
state variable for each connection, which we refer to as
CongestionWindow (but you will often see it called cwnd in the
literature, based on the variable name used in the code). It is used
by the source to limit how much data it is allowed to have in transit
at a given time.
The congestion window is congestion control’s counterpart to flow control’s advertised window. The TCP sender is modified such that the maximum number of bytes of unacknowledged data allowed is now the minimum of the congestion window and the advertised window. Thus, using the variables defined in Chapter 2, TCP’s effective window is revised as follows:
That is, MaxWindow replaces AdvertisedWindow in the calculation
of EffectiveWindow. Thus, a TCP source is allowed to send no
faster than the slowest component—the network or the destination
host—can accommodate.
The problem, of course, is how TCP comes to learn an appropriate value
for CongestionWindow. Unlike the AdvertisedWindow, which is
sent by the receiving side of the connection, there is no one to send
a suitable CongestionWindow to the sending side of TCP. The answer
is that the TCP source sets the CongestionWindow based on the
level of congestion it perceives to exist in the network. This
involves decreasing the congestion window when the level of congestion
goes up and increasing the congestion window when the level of
congestion goes down. Taken together, the mechanism is commonly called
additive increase/multiplicative decrease (AIMD) due to the
approach it adopts.
The key question then becomes: how does the source determine that the
network is congested and that it should decrease the congestion
window? The answer is based on the observation that the main reason
packets are not delivered, and a timeout results, is that a packet was
dropped due to congestion. It is rare that a packet is dropped because
of an error during transmission. Therefore, TCP interprets timeouts as
a sign of congestion and reduces the rate at which it is transmitting.
Specifically, each time a timeout occurs, the source sets
CongestionWindow to half of its previous value. This halving of
the CongestionWindow for each timeout corresponds to the
“multiplicative decrease” part of AIMD.
Although CongestionWindow is defined in terms of bytes, it is
easiest to understand multiplicative decrease if we think in terms of
whole packets. For example, suppose the CongestionWindow is
currently set to 16 packets. If a loss is detected,
CongestionWindow is set to 8. (Normally, a loss is detected when a
timeout occurs, but as we see below, TCP has another mechanism to
detect dropped packets.) Additional losses cause CongestionWindow
to be reduced to 4, then 2, and finally to 1 packet.
CongestionWindow is not allowed to fall below the size of a single
packet, which we know from Chapter 2 to be the MSS.
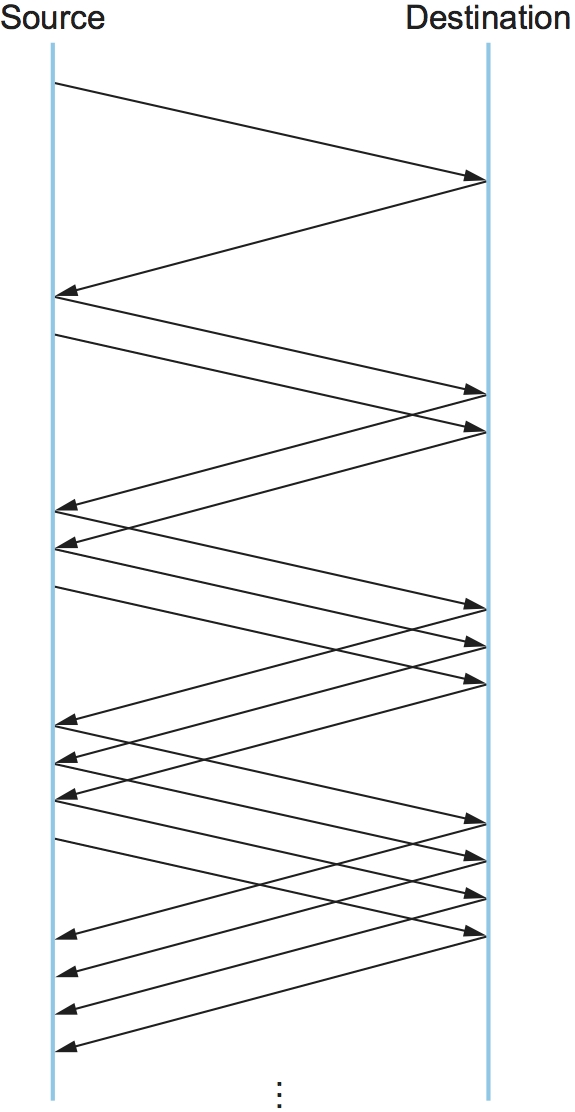
Figure 22. Packets in transit during additive increase, with one packet being added each RTT.
A congestion-control strategy that only decreases the window size is
obviously too conservative. We also need to be able to increase the
congestion window to take advantage of newly available capacity in the
network. This is the “additive increase” part of AIMD, and it works as
follows. Every time the source successfully sends a
CongestionWindow’s worth of packets—that is, each packet sent
out during the last round-trip time (RTT) has been ACKed—it adds the
equivalent of 1 packet to CongestionWindow. This linear increase
is illustrated in Figure 22.
In practice, TCP does not wait for an entire window’s worth of ACKs to
add 1 packet’s worth to the congestion window, but instead increments
CongestionWindow by a little for each ACK that
arrives. Specifically, the congestion window is incremented as follows
each time an ACK arrives:
That is, rather than incrementing CongestionWindow by an entire
MSS bytes each RTT, we increment it by a fraction of MSS every
time an ACK is received. Assuming that each ACK acknowledges the receipt
of MSS bytes, then that fraction is MSS/CongestionWindow.
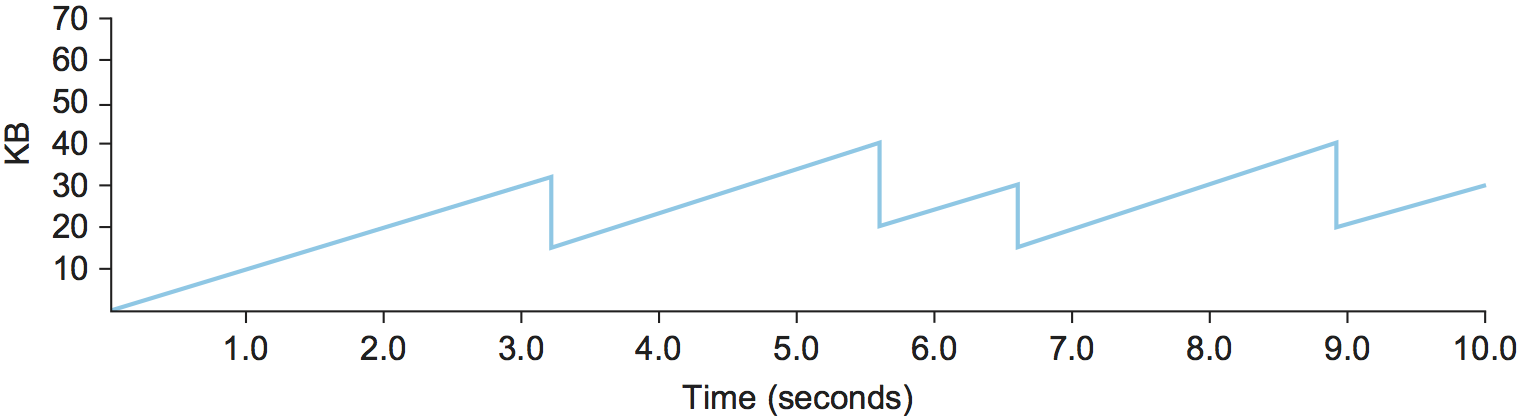
Figure 23. Typical TCP sawtooth pattern.
This pattern of continually increasing and decreasing the congestion
window continues throughout the lifetime of the connection. In fact,
if you plot the current value of CongestionWindow as a function of
time, you get a sawtooth pattern, as illustrated in Figure 23. The important concept to understand about AIMD is
that the source is willing to reduce its congestion window at a much
faster rate than it is willing to increase its congestion window. One
could imagine an additive increase/additive decrease strategy in
which the window would be increased by 1 packet when an ACK arrives
and decreased by 1 when a timeout occurs, but this turns out to be too
aggressive. Responding quickly to congestion
is important to stability.
An intuitive explanation for why TCP decreases the window aggressively and increases it conservatively is that the consequences of having too large a window are compounding. This is because when the window is too large, packets that are dropped will be retransmitted, making congestion even worse. It is important to get out of this state quickly. You can think of AIMD as gently increasing the data in flight to probe for the level at which congestion begins, then aggressively stepping back from the brink of congestion collapse when that level is detected by a timeout.
Finally, since a timeout is an indication of congestion that triggers multiplicative decrease, TCP needs the most accurate timeout mechanism it can afford. We already covered TCP’s timeout mechanism in Section 4.1, but recall that timeouts are set as a function of both the average RTT and the deviation in that average.
4.3 Slow Start
The additive increase mechanism just described is a reasonable approach to use when the source is operating close to the available capacity of the network, but it takes too long to ramp up a connection when it is starting from scratch. TCP therefore provides a second mechanism, counter-intuitively called slow start, which is used to increase the congestion window rapidly from a cold start. Slow start effectively increases the congestion window exponentially, rather than linearly.
Specifically, the source starts out by setting CongestionWindow to
one packet. When the ACK for this packet arrives, TCP adds 1 to
CongestionWindow and then sends two packets. Upon receiving the
corresponding two ACKs, TCP increments CongestionWindow by 2—one
for each ACK—and next sends four packets. The end result is that TCP
effectively doubles the number of packets it has in transit every RTT.
Figure 24 shows the growth in the number
of packets in transit during slow start. Compare this to the linear
growth of additive increase illustrated in Figure 22.
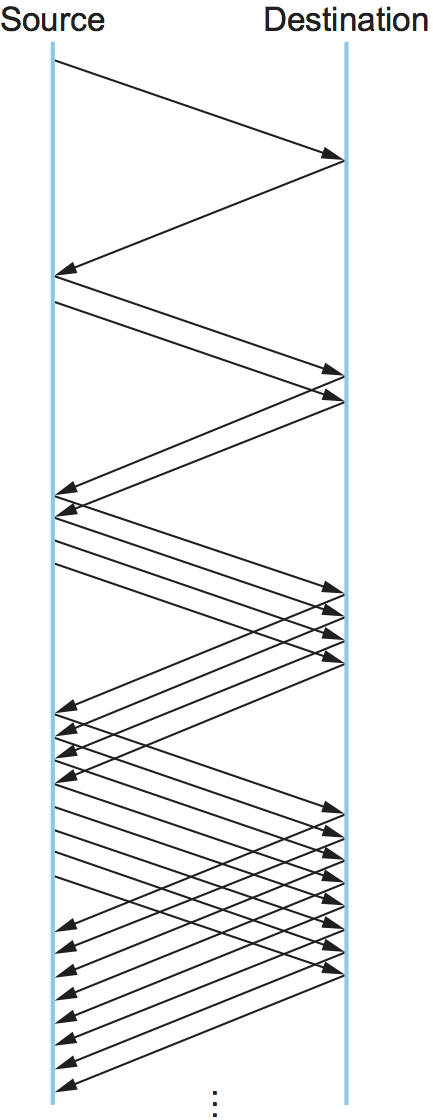
Figure 24. Packets in transit during slow start.
Why any exponential mechanism would be called “slow” is puzzling at first, but it makes sense in its historical context. We need to compare slow start not against the linear mechanism of the previous section, but against the original behavior of TCP. Consider what happens when a connection is established and the source first starts to send packets—that is, when it currently has no packets in transit. If the source sends as many packets as the advertised window allows—which is exactly what TCP did before slow start was developed—then even if there is a fairly large amount of bandwidth available in the network, the routers may not be able to consume this burst of packets. It all depends on how much buffer space is available at the routers. Slow start was therefore designed to space packets out so that this burst does not occur. In other words, even though its exponential growth is faster than linear growth, slow start is much “slower” than sending an entire advertised window’s worth of data all at once.
There are actually two different situations in which slow start runs.
The first is at the very beginning of a connection, at which time the
source has no idea how many packets it is going to be able to have in
transit at a given time. (Keep in mind that today TCP runs over
everything from 1-Mbps links to 40-Gbps links, so there is no way for
the source to know the network’s capacity.) In this situation, slow
start continues to double CongestionWindow each RTT until there is a
loss, at which time a timeout causes multiplicative decrease to divide
CongestionWindow by 2.
The second situation in which slow start is used is a bit more subtle; it occurs when the connection goes dead while waiting for a timeout to occur. Recall how TCP’s sliding window algorithm works—when a packet is lost, the source eventually reaches a point where it has sent as much data as the advertised window allows, and so it blocks while waiting for an ACK that will not arrive. Eventually, a timeout happens, but by this time there are no packets in transit, meaning that the source will receive no ACKs to “clock” the transmission of new packets. The source will instead receive a single cumulative ACK that reopens the entire advertised window, but, as explained above, the source then uses slow start to restart the flow of data rather than dumping a whole window’s worth of data on the network all at once.
Although the source is using slow start again, it now knows more
information than it did at the beginning of a connection. Specifically,
the source has a current (and useful) value of CongestionWindow;
this is the value of CongestionWindow that existed prior to the last
packet loss, divided by 2 as a result of the loss. We can think of this
as the target congestion window. Slow start is used to rapidly
increase the sending rate up to this value, and then additive increase
is used beyond this point. Notice that we have a small bookkeeping
problem to take care of, in that we want to remember the target
congestion window resulting from multiplicative decrease as well as the
actual congestion window being used by slow start. To address this
problem, TCP introduces a temporary variable to store the target window,
typically called CongestionThreshold, that is set equal to the
CongestionWindow value that results from multiplicative decrease.
The variable CongestionWindow is then reset to one packet, and it is
incremented by one packet for every ACK that is received until it
reaches CongestionThreshold, at which point it is incremented by one
packet per RTT.
In other words, TCP increases the congestion window as defined by the following code fragment:
{
u_int cw = state->CongestionWindow;
u_int incr = state->maxseg;
if (cw > state->CongestionThreshold)
incr = incr * incr / cw;
state->CongestionWindow = MIN(cw + incr, TCP_MAXWIN);
}
where state represents the state of a particular TCP connection and
defines an upper bound on how large the congestion window is allowed to
grow.
Figure 25 traces how TCP’s CongestionWindow
increases and decreases over time and serves to illustrate the
interplay of slow start and additive increase/multiplicative
decrease. This trace was taken from an actual TCP connection and shows
the current value of CongestionWindow—the colored line—over time.
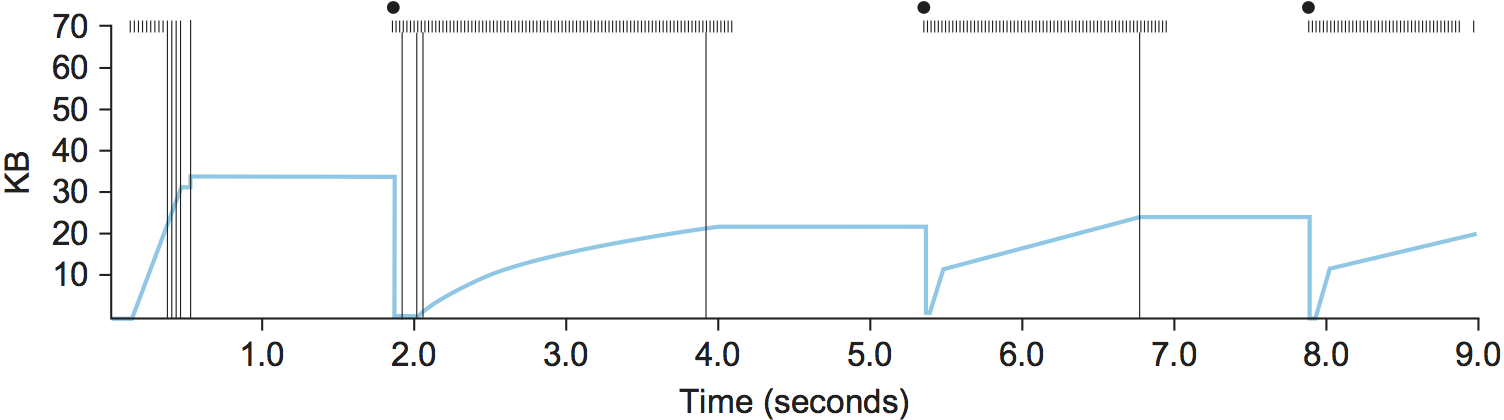
Figure 25. Behavior of TCP congestion control. Colored line = value of CongestionWindow over time; solid bullets at top of graph = timeouts; hash marks at top of graph = time when each packet is transmitted; vertical bars = time when a packet that is eventually retransmitted was first transmitted.
There are several things to notice about this trace. The first is the
rapid increase in the congestion window at the beginning of the
connection. This corresponds to the initial slow start phase. The slow
start phase continues until several packets are lost at about 0.4
seconds into the connection, at which time CongestionWindow flattens
out at about 34 KB. (Why so many packets are lost during slow start is
discussed below.) The reason why the congestion window flattens is that
there are no ACKs arriving, due to the fact that several packets were
lost. In fact, no new packets are sent during this time, as denoted by
the lack of hash marks at the top of the graph. A timeout eventually
happens at approximately 2 seconds, at which time the congestion window
is divided by 2 (i.e., cut from approximately 34 KB to around 17 KB) and
CongestionThreshold is set to this value. Slow start then causes
CongestionWindow to be reset to one packet and to start ramping up
from there.
There is not enough detail in the trace to see exactly what happens when
a couple of packets are lost just after 2 seconds, so we jump ahead to
the linear increase in the congestion window that occurs between 2 and
4 seconds. This corresponds to additive increase. At about 4 seconds,
CongestionWindow flattens out, again due to a lost packet. Now, at
about 5.5 seconds:
A timeout happens, causing the congestion window to be divided by 2, dropping it from approximately 22 KB to 11 KB, and
CongestionThresholdis set to this amount.CongestionWindowis reset to one packet, as the sender enters slow start.Slow start causes
CongestionWindowto grow exponentially until it reachesCongestionThreshold.CongestionWindowthen grows linearly.
The same pattern is repeated at around 8 seconds when another timeout occurs.
We now return to the question of why so many packets are lost during the initial slow start period. At this point, TCP is attempting to learn how much bandwidth is available on the network. This is a difficult task. If the source is not aggressive at this stage—for example, if it only increases the congestion window linearly—then it takes a long time for it to discover how much bandwidth is available. This can have a dramatic impact on the throughput achieved for this connection. On the other hand, if the source is aggressive at this stage, as TCP is during exponential growth, then the source runs the risk of having half a window’s worth of packets dropped by the network.
To see what can happen during exponential growth, consider the situation in which the source was just able to successfully send 16 packets through the network, causing it to double its congestion window to 32. Suppose, however, that the network happens to have just enough capacity to support 16 packets from this source. The likely result is that 16 of the 32 packets sent under the new congestion window will be dropped by the network; actually, this is the worst-case outcome, since some of the packets will be buffered in some router. This problem will become increasingly severe as the bandwidth-delay product of networks increases. For example, a bandwidth-delay product of 1.8 MB means that each connection has the potential to lose up to 1.8 MB of data at the beginning of each connection. Of course, this assumes that both the source and the destination implement the “big windows” extension.
Alternatives to slow start, whereby the source tries to estimate the available bandwidth by more sophisticated means, have also been explored. One example is called quick-start. The basic idea is that a TCP sender can ask for an initial sending rate greater than slow start would allow by putting a requested rate in its SYN packet as an IP option. Routers along the path can examine the option, evaluate the current level of congestion on the outgoing link for this flow, and decide if that rate is acceptable, if a lower rate would be acceptable, or if standard slow start should be used. By the time the SYN reaches the receiver, it will contain either a rate that was acceptable to all routers on the path or an indication that one or more routers on the path could not support the quick-start request. In the former case, the TCP sender uses that rate to begin transmission; in the latter case, it falls back to standard slow start. If TCP is allowed to start off sending at a higher rate, a session could more quickly reach the point of filling the pipe, rather than taking many round-trip times to do so.
Clearly one of the challenges to this sort of enhancement to TCP is that it requires substantially more cooperation from the routers than standard TCP does. If a single router in the path does not support quick-start, then the system reverts to standard slow start. Thus, it could be a long time before these types of enhancements could make it into the Internet; for now, they are more likely to be used in controlled network environments (e.g., research networks).
4.4 Fast Retransmit and Fast Recovery
The mechanisms described so far were part of the original proposal to add congestion control to TCP, and they have collectively become known as TCP Tahoe because they were included in the Tahoe release of 4.3 BSD Unix in 1988. Once widely deployed, experience revealed some problems in Tahoe that were subsequently addressed by TCP Reno (part of the 4.3BSD-Reno release) in early 1990. This section describes that experience and Reno’s approach to addressing it.
In short, the coarse-grained implementation of TCP timeouts led to long periods of time during which the connection went dead while waiting for a timer to expire. A heuristic, called fast retransmit, sometimes triggers the retransmission of a dropped packet sooner than the regular timeout mechanism. The fast retransmit mechanism does not replace regular timeouts; it just adds another way of detecting lost packets that can be more timely.
The idea is that every time a data packet arrives at the receiving side, the receiver responds with an acknowledgment, even if this sequence number has already been acknowledged. Thus, when a packet arrives out of order—when TCP cannot yet acknowledge the data the packet contains because earlier data has not yet arrived—TCP resends the same acknowledgment it sent the last time.
This second transmission of the same acknowledgment is called a duplicate ACK. When the sending side sees a duplicate ACK, it knows that the other side must have received a packet out of order, which suggests that an earlier packet might have been lost. Since it is also possible that the earlier packet has only been delayed rather than lost, the sender waits until it sees some number of duplicate ACKs (in practice, three) and then retransmits the missing packet. The built-in assumption here, which is well tested in practice, is that out-of-order packets are less common by far than lost packets.
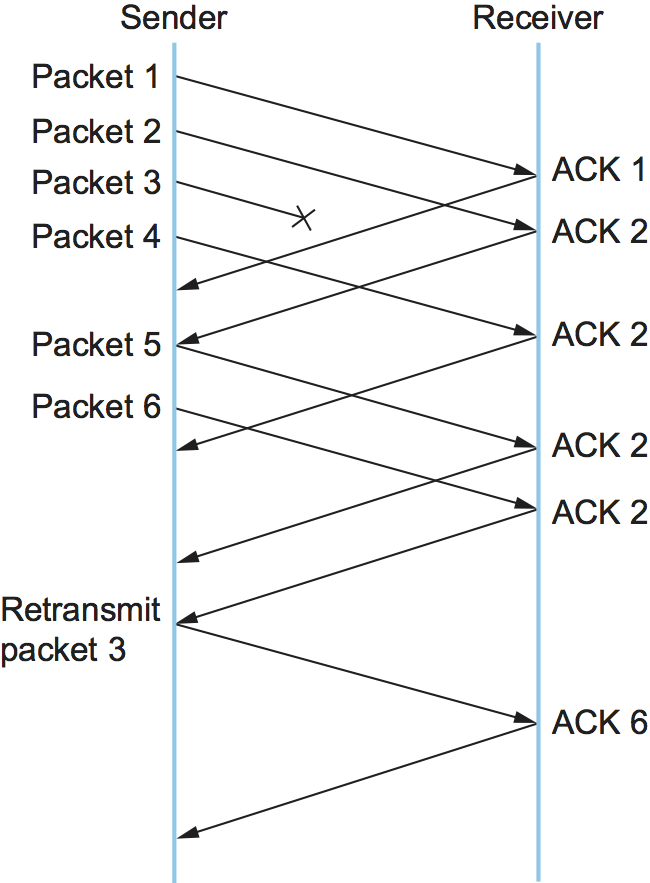
Figure 26. Fast retransmit based on duplicate ACKs.
Figure 26 illustrates how duplicate ACKs lead to a fast retransmit. In this example, the destination receives packets 1 and 2, but packet 3 is lost in the network. Thus, the destination will send a duplicate ACK for packet 2 when packet 4 arrives, again when packet 5 arrives, and so on. (To simplify this example, we think in terms of packets 1, 2, 3, and so on, rather than worrying about the sequence numbers for each byte.) When the sender sees the third duplicate ACK for packet 2—the one sent because the receiver had gotten packet 6—it retransmits packet 3. Note that when the retransmitted copy of packet 3 arrives at the destination, the receiver then sends a cumulative ACK for everything up to and including packet 6 back to the source.
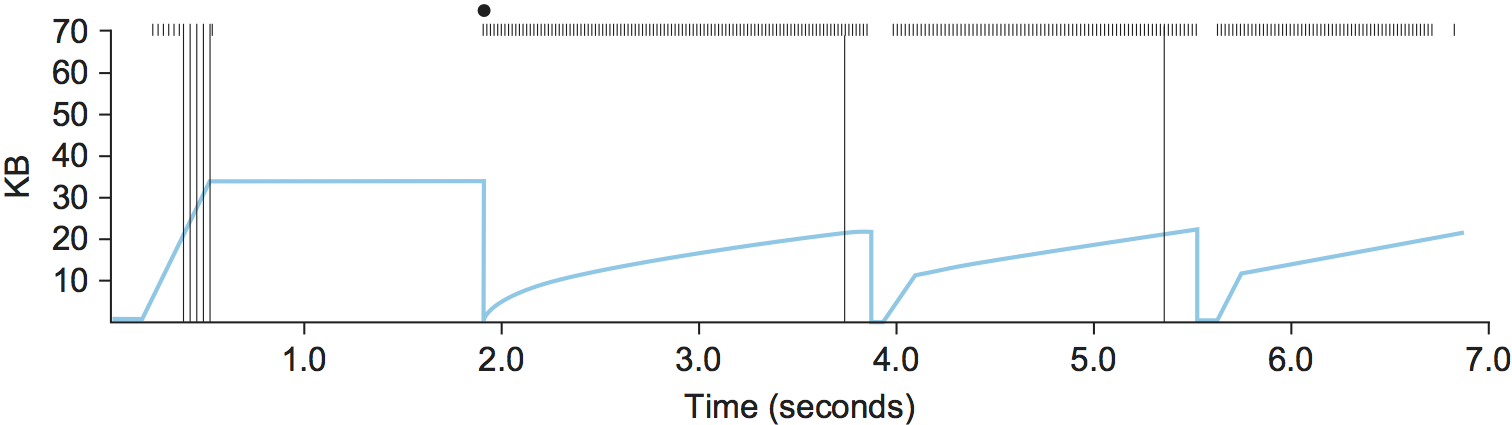
Figure 27. Trace of TCP with fast retransmit. Colored line = CongestionWindow; solid bullet = timeout; hash marks = time when each packet is transmitted; vertical bars = time when a packet that was eventually retransmitted was first transmitted.
Figure 27 illustrates the behavior of a version of TCP with the fast retransmit mechanism. It is interesting to compare this trace with that given in Figure 25, where fast retransmit was not implemented—the long periods during which the congestion window stays flat and no packets are sent have been eliminated. In general, this technique is able to eliminate about half of the coarse-grained timeouts on a typical TCP connection, resulting in roughly a 20% improvement in the throughput over what could otherwise have been achieved. Notice, however, that the fast retransmit strategy does not eliminate all coarse-grained timeouts. This is because for a small window size there will not be enough packets in transit to cause enough duplicate ACKs to be delivered. Given enough lost packets—for example, as happens during the initial slow start phase—the sliding window algorithm eventually blocks the sender until a timeout occurs. In practice, TCP’s fast retransmit mechanism can detect up to three dropped packets per window.
There is one further improvement we can make. When the fast retransmit mechanism signals congestion, rather than drop the congestion window all the way back to one packet and run slow start, it is possible to use the ACKs that are still in the pipe to clock the sending of packets. This mechanism, which is called fast recovery, effectively removes the slow start phase that happens between when fast retransmit detects a lost packet and additive increase begins. For example, fast recovery avoids the slow start period between 3.8 and 4 seconds in Figure 27 and instead simply cuts the congestion window in half (from 22 KB to 11 KB) and resumes additive increase. In other words, slow start is only used at the beginning of a connection and whenever a coarse-grained timeout occurs. At all other times, the congestion window is following a pure additive increase/multiplicative decrease pattern.
4.5 Incremental Enhancements
If a study of TCP congestion control teaches us one thing, it’s how complex the problem is, and how many details you have to get right. This happens only through a sequence of incremental improvements that are the result of experience. The following gives two additional examples of that lesson.
4.5.1 TCP SACK
The original TCP specification uses cumulative acknowledgments, meaning that the receiver acknowledges the last packet it received prior to any lost packets. You can think of the receiver having a collection of received packets where any lost packets are represented by holes in the received byte stream. With the original specification, it’s only possible to tell the sender where the first hole starts, even if several packets have been lost. Intuitively, this lack of detail could limit the sender’s ability to respond effectively to packet loss. The approach taken to address this is called selective acknowledgments or SACK. SACK is another optional extension to TCP that was first proposed soon after the early work of Jacobson and Karels but took some years to gain acceptance, as it was hard to prove that it would be beneficial.
Without SACK, there are only two reasonable strategies for a sender to adopt when segments are received out-of-order. The pessimistic strategy responds to a duplicate ACK or a timeout by retransmitting not just the segment that was clearly lost (the first packet missing at the receiver), but any segments transmitted subsequently. In effect, the pessimistic strategy assumes the worst: that all those segments were lost. The disadvantage of the pessimistic strategy is that it may unnecessarily retransmit segments that were successfully received the first time. The other strategy is to respond to a loss signal (timeout or duplicate ACK) by retransmitting only the segment that triggered that signal. This optimistic approach assumes the rosiest scenario: that only the one segment has been lost. The disadvantage of the optimistic strategy is that it is very slow to recover when a series of consecutive segments has been lost, as might happen when there is congestion. It is slow because each segment’s loss is not discovered until the sender receives an ACK for its retransmission of the previous segment. This means it consumes one RTT per segment until it has retransmitted all the segments in the lost series. With the SACK option, a better strategy is available to the sender: retransmit just the segments that fill the gaps between the segments that have been selectively acknowledged.
SACK is first negotiated at the start of a connection by the sender
telling the receiver that it can handle the SACK option. When the SACK
option is used, the receiver continues to acknowledge segments
normally—the meaning of the Acknowledge field does not change—but
it also extends the header with additional acknowledgments for any
blocks received out-of-order. This allows the sender to identify the
holes that exist at the receiver, and retransmit just the segments
that are missing instead of all the segments that follow a dropped
segment.
SACK was shown to improve the performance of TCP Reno particularly in the case where multiple packets were dropped in a single RTT, as would be expected (since cumulative ACK and SACK are the same thing when only one packet is dropped). This scenario became more likely over time as bandwidth-delay products increased, leaving more packets in the pipe for a given RTT. Hence SACK, which became a proposed IETF standard in 1996, was a timely addition to TCP.
4.5.2 NewReno
Starting with some research by Janey Hoe at MIT in the mid-1990s, the enhancement known as NewReno incrementally improves the performance of TCP by making more intelligent decisions about which packets to retransmit under certain packet loss conditions.
Further Reading
J. Hoe. Improving the start-up behavior of a congestion control scheme for TCP. SIGCOMM ‘96. August 1996.
The key insight behind NewReno is that even without SACK, duplicate ACKs can convey information to the sender about how many packets have been dropped and which ones they were, so that the sender can make more intelligent choices about when to retransmit a packet. Furthermore, in the presence of multiple losses from a single window, NewReno can avoid the multiple halvings of the congestion window that occurred in prior versions.
The details of NewReno are extensive, but the intuition is as follows. If a single packet is lost, then after three duplicate ACKs, the sender will retransmit the lost packet. When it arrives, the receiver will acknowledge all the outstanding data, as it has now filled the one hole in its receive buffer. Conversely, if multiple packets were lost, the first ACK after that retransmitted packet is received will only partially cover the outstanding packets. From this, the sender can infer that there were more packets lost, and immediately start to try to fill the gaps by sending the next packet that has not yet been acknowledged. This can lead to fewer timeouts and hence less idle time and fewer reductions in the congestion window.
It’s worth noting that NewReno was documented in three RFCs published between 1999 and 2012, each one of which fixed some issues in its predecessor’s algorithms. This is a case study in how complex it can be to understand the fine detail of congestion control (especially with respect to the subtleties of TCP’s retransmission mechanism), adding to the challenge of getting new algorithms into deployment.
4.6 TCP CUBIC
It should be clear by now that trying to find the appropriate rate at which to send traffic into the network is at the heart of congestion control, and that it’s possible to err in either direction. Send too little traffic and the network is underutilized leading to poor application performance. Send too much and the network becomes congested, leading to congestion collapse in the worst case. Between these two failure modes, sending too much traffic is generally the more serious, because of the way congestion can quickly compound itself as lost packets are retransmitted. The AIMD approach that is built into Tahoe, Reno and NewReno reflects this: increase the window slowly (additive increase) and decrease it quickly (multiplicative decrease) in an effort to step back from the brink of congestion collapse before it gets too severe. But in high bandwidth-delay environments, the cost of being too conservative in probing for congestion is quite high, as it can take many RTTs before the “pipe is full”. So this has led to some rethinking on how to probe for the appropriate window size.
This idea that the window should open quickly at some times and more slowly at others was captured in a new approach called Binary Increase Congestion Control (BIC). Rather than abruptly switching from exponential window growth to linear, as TCP Reno does, BIC effectively does a binary search for the “right” window size. After a packet loss, the congestion window is cut by a multiplicative factor \(\beta\). With each successful iteration of sending packets at the new window size, the window is increased to the midpoint of its current value and the old value that caused congestion. In this way, it asymptotes towards the old value—first quickly then slowly. (Taken to the extreme, the window would never get back to its old value—see Zeno’s paradox—but when it gets within a certain threshold it is set to the old value).
At this point, if there is no congestion, we can conclude that the network conditions have changed, and it is OK to probe for a new congestion window size. BIC does this first slowly and then more rapidly. You can see the approximate shape of how BIC grows its window in Figure 28, asymptoting towards \(W_{max}\) (the old congestion window prior to the last loss) and then moving beyond it.
BIC eventually evolved into a new variant called CUBIC, which today is the default congestion control algorithm distributed with Linux. CUBIC improved upon BIC in a number of ways, one of which was to use a smooth curve described by a cubic function rather than the piecewise linear function of BIC. More on this below.
Another important aspect of CUBIC’s approach is to adjust its congestion window at regular intervals, based on the amount of time that has elapsed since the last congestion event (e.g., the arrival of a duplicate ACK), rather than only when ACKs arrive (the latter being a function of RTT). This allows CUBIC to behave fairly when long-RTT flows compete with short-RTT flows, which have ACKs arriving more frequently. This is an interesting departure from prior versions of TCP, in which a flow with a short RTT holds a definite advantage in terms of the share of a bottleneck link it will obtain.
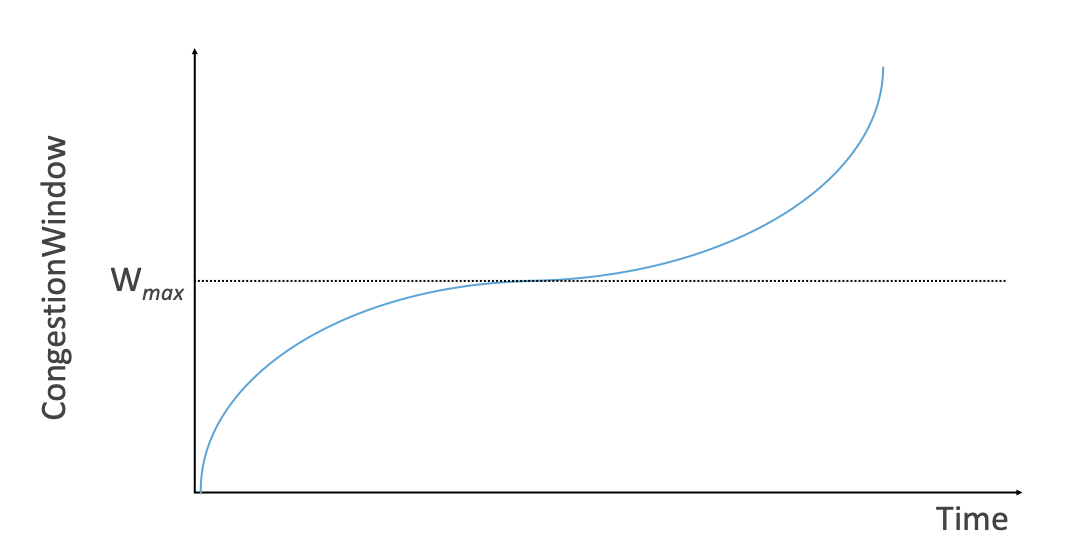
Figure 28. Generic cubic function illustrating the change in the congestion window as a function of time.
The cubic function, shown in Figure 28, has three phases: slowing growth, flatten plateau, increasing growth. The maximum congestion window size achieved just before the last congestion event is the initial target (denoted \(\mathsf{W}_{max}\)). You can see how the window growth starts fast but slows as you get close to \(\mathsf{W}_{max}\); then there is a phase of cautious growth when close to \(\mathsf{W}_{max}\), and finally a phase of probing for a new achievable \(\mathsf{W}_{max}\).
Specifically, CUBIC computes the congestion window (CongestionWindow) as a function of time
(t) since the last congestion event
where
C is a scaling constant and \(\beta\) is the multiplicative decrease factor. CUBIC sets the latter to 0.7 rather than the 0.5 that standard TCP uses. Looking back at Figure 28, CUBIC is often described as shifting between a concave function to being convex (whereas standard TCP’s additive function is only convex).
Interestingly, CUBIC is either more aggressive or less aggressive than earlier variants of TCP, depending on the conditions. Short RTT TCP Reno flows tend to be effective in acquiring bottleneck bandwidth, so CUBIC includes a “TCP-friendly” mode where it aims to be just as aggressive as TCP Reno. But in other circumstances—notably high bandwidth-delay networks—CUBIC will be able to obtain a bigger share of the bottleneck bandwidth because CUBIC is increasing its window size more quickly. This brings us back to the discussion of Section 3.3 as to whether “fairness” to incumbent algorithms is the right design goal. Ultimately, CUBIC was extensively analyzed, showed good performance under many conditions without causing undue harm, and has been widely deployed.
Further Reading
S. Ha, I. Rhee, and L. Xu. CUBIC: a New TCP-friendly High-speed TCP Variant. ACM SIGOPS Operating Systems Review, July 2008.