Chapter 3: Design Space
With the architectural foundation of TCP/IP in place, we are ready to explore the design space for addressing congestion. But to do this, it is helpful to first take a step back and consider the bigger picture. The Internet is a complex arrangement of compute, storage, and communication resources that is shared among millions of users. The challenge is how to assign those resources—specifically switching capacity, buffer space, and link bandwidth—to end-to-end packet flows.
Because the Internet originally adopted a best-effort service model, and users (or more precisely, TCP running on their behalf) were free to send as many packets into the network as they could generate, it was not surprising that the Internet eventually suffered from the tragedy of the commons. And with users starting to experience congestion collapse, the natural response was to try to control it. Hence the term congestion control, which can be viewed as an implicit mechanism for allocating resources. It is implicit in the sense that as the control mechanism detects resources becoming scarce, it reacts in an effort to alleviate congestion.
A network service model in which resources are explicitly allocated to packet flows is the obvious alternative; for example, an application could make an explicit request for resources before sending traffic. The best-effort assumption of IP meant such an approach was not immediately viable at the time congestion became a serious issue. Subsequent work was done to retrofit more explicit resource allocation mechanisms to the Internet’s best-effort delivery model, including the ability to make Quality-of-Service (QoS) guarantees. It is instructive to consider the Internet’s approach to congestion in the context of such efforts. The first section does so as it explores the set of design decisions that underlie the control mechanisms outlined in this book. We then define the criteria by which different congestion-control mechanisms can be quantitatively evaluated and compared.
3.1 Implementation Choices
We start by introducing four implementation choices that a congestion control mechanism faces, and the design rationale behind the decisions that were made for TCP/IP. Some of the decisions were “obvious” given the circumstances under which they were made, but for completeness—and because the Internet’s continual evolution means circumstances change—it is prudent to consider them all.
3.1.1 Centralized versus Distributed
In principle, the first design decision is whether a network’s approach to resource allocation is centralized or distributed. In practice, the Internet’s scale—along with the autonomy of the organizations that connect to it—dictated a distributed approach. Indeed, distributed management of resources was an explicitly stated goal of the Internet’s design, as articulated by Dave Clark. But acknowledging this default decision is important for two reasons.
Further Reading
D. Clark, The Design Philosophy of the DARPA Internet Protocols. ACM SIGCOMM, 1988.
First, while the Internet’s approach to congestion control is distributed across its millions of hosts and routers, it is fair to think of them as cooperatively trying to achieve a globally optimal solution. From this perspective, there is a shared objective function, and all the elements are implementing a distributed algorithm to optimize that function. The various mechanisms described throughout this book are simply defining different objective functions, where a persistent challenge has been how to think about competing objective functions when multiple mechanisms have been deployed.
Second, while a centralized approach is not practical for the Internet as a whole, it can be appropriate for limited domains. For example, a logically centralized controller could collect information about the state of the network’s links and switches, compute a globally optimal allocation, and then advise (or even police) end hosts as to how much capacity is available to each of them. Such an approach would certainly be limited by the time-scale in which the centralized controller could be responsive to changes in the network, but it has been successfully applied to the coarse-grained allocation decisions made by traffic engineering mechanisms like B4 and SWAN. Exactly where one draws a line between coarse-grain traffic engineering decisions and fine-grain congestion control decisions is not clear, but it’s good to keep an open mind about the spectrum of options that are available.
Further Reading
S. Jain, et al. B4: Experience with a Globally-Deployed Software Defined WAN. ACM SIGCOMM, August 2013.
Centralized control has also been used effectively in datacenters, which are an interesting environment for congestion control. First, they have very low RTTs (for traffic between servers in the datacenter, if not for flows heading in or out of the datacenter). Second, in many cases a datacenter can be treated as a greenfield, raising the possibility to try new approaches that don’t have to coexist fairly with incumbent algorithms. Fastpass, developed in a collaboration between MIT and Facebook researchers, is a good example of such a centralized approach.
Further Reading
J. Perry, et al. Fastpass: A Centralized “Zero-Queue” Datacenter Network. ACM SIGCOMM, August 2014.
3.1.2 Router-Centric versus Host-Centric
Given a distributed approach to resource allocation, the next question is whether to implement the mechanism inside the network (i.e., at the routers or switches) or at the edges of the network (i.e., in the hosts, perhaps as part of the transport protocol). This is not strictly an either/or situation. Both locations are involved, and the real issue is where the majority of the burden falls. Individual routers always take responsibility for deciding which packets to forward and which packets to drop. However, there is a range of options in how much the router involves the end hosts in specifying how this decision is made, or learning how this decision was made.
At one end of the spectrum, routers can allow hosts to reserve capacity and then ensure each flow’s packets are delivered accordingly. They might do this, for example, by implementing a signalling protocol along with Fair Queuing, accepting new flows only when there is sufficient capacity, and policing hosts to make sure their flows stay within their reservations. This would correspond to a reservation-based approach in which the network is able to make QoS guarantees. We consider this out-of-scope for the purpose of this book.
At the other end of the spectrum is a host-centric approach. The router makes no guarantees and offers no explicit feedback about the available capacity (i.e., silently drops packets when its buffers are full) and it is the host’s responsibility to observe the network conditions (e.g., how many packets they are successfully getting through the network) and adjust its behavior accordingly.
In the middle, routers can take more proactive action to assist the end hosts in doing their job, but not by reserving buffer space. This involves the router sending feedback to the end hosts when its buffers are full. We describe some of these forms of Active Queue Management (AQM) in Chapter 6, but the host-centric mechanisms described in the next two chapters assume routers silently tail-drop packets when their buffers are full.
Historically, the host-centric approach has been implemented in the transport layer—usually by TCP, or by some other transport protocol that mimics TCP’s algorithm, such as DCCP (datagram congestion control protocol) or QUIC (a relatively recent transport protocol designed for HTTP-based applications). However, it is also possible to implement congestion control in the application itself. DASH (Dynamic Adaptive Streaming over HTTP) is an example, although it is best viewed as a combination of congestion control in the transport layer (since it runs over TCP) and the application layer. Based on measured network performance, the server that is streaming video to a client switches among a range of different video encodings, thus changing the rate at which data is sent into the HTTP stream. In effect, TCP tries to find a sustainable bandwidth for the flow, and then the application adapts its sending rate to fully leverage that rate without sending more data than can be sustained under the current network conditions. Primary responsibility for congestion control falls to TCP, but the application aims to keep the pipe full while also maintaining a good user experience.
3.1.3 Window-Based versus Rate-Based
Having settled on a host-centric approach, the next implementation choice is whether the mechanism is window-based or rate-based. TCP uses a window-based mechanism to implement flow control, so the design decision for TCP congestion control seems obvious. And in fact, the congestion-control mechanisms described in Chapter 4 are centered around an algorithm for computing a congestion window, where the sender is throttled by whichever is lesser: the advertised flow-control window or the computed congestion-control window.
But it is also possible to compute the rate at which the network is able to deliver packets, and to pace transmissions accordingly. The observed rate is just the number of bytes delivered over some time period, such as the measured RTT. We point out this duality between rates and windows because a rate-based approach is more appropriate for multimedia applications that generate data at some average rate and which need at least some minimum throughput to be useful. For example, a video codec might generate video at an average rate of 1 Mbps with a peak rate of 2 Mbps.
A rate-based approach is the logical choice in a reservation-based system that supports different QoS levels, but even in a best-effort network like the Internet, it is possible to implement an adaptive rate-based congestion-control mechanism that informs the application when it needs to adjust it transmission rate, for example by adjusting its codec. This is the core idea of TCP-friendly rate control (TFRC), which extends the concepts of TCP congestion avoidance to applications that more naturally send packets at a specific rate (e.g., the bitrate produced by a video codec at a given quality level). TFRC is typically used in conjunction with RTP, a transport protocol designed for real-time applications. We will see examples of such mechanisms in Chapter 7.
Finally, one of the recent advances in TCP congestion control is BBR (Bottleneck Bandwidth and RTT) which uses a combination of window-based and rate-based control, in an effort to limit the build up of queues within the network. We examine this approach in some detail in Chapter 5.
3.1.4 Control-based versus Avoidance-based
The final implementation choice we draw attention to is somewhat subtle. The challenge is for the end-host, based on feedback and observations, to compute how much capacity is available in the network, and adjust its sending rate accordingly. There are two general strategies for doing this: an aggressive approach that purposely sends packets at a rate that causes packet loss and then responds to it, and a conservative approach that tries to detect the onset of queue build-up and slow down before they actually overflow. We refer to the mechanisms of the first type as control-based, and we refer to mechanisms of the second type as avoidance-based.
Further Reading
R. Jain and K. K. Ramakrishnan. Congestion Avoidance in Computer Networks with a Connectionless Network Layer: Concepts, Goals and Methodology.. Computer Networking Symposium, April 1988.
This distinction was first called out by Raj Jain and K.K. Ramakrishnan Jain in 1988. It is often overlooked—and the term “congestion control” is used generically to refer to both—but our take is that the distinction represents an important difference, and so we will call it out when appropriate. Admittedly, we will also fall back to the generic use of “congestion control” when the distinction is not critical to the discussion.
Also note that the approaches we call “control-based” and “avoidance-based” are sometimes referred to as loss-based and delay-based, respectively, according to the criteria each uses as a signal that the congestion window needs to be adjusted. The former adjusts the window when it detects a loss and the latter adjusts the window when it detects a change in the delay gradient. When viewed from this perspective, each of the algorithms introduced over the next four chapters effectively refines the fidelity of these signals in one way or another.
3.2 Evaluation Criteria
Having identified the set of design decisions that go into crafting a congestion-control mechanism, the next question is whether any given solution is good or not. Recall that in Chapter 1 we posed the question of how a network effectively and fairly allocates its resources. This suggests at least two broad measures by which a resource allocation scheme can be evaluated. We consider each in turn.
3.2.1 Effectiveness
A good starting point for evaluating the effectiveness of a congestion-control mechanism is to consider the two principal metrics of networking: throughput and delay. Clearly, we want as much throughput and as little delay as possible. Unfortunately, these goals can be at odds with each other. One way to increase throughput is to allow as many packets into the network as possible, so as to drive the utilization of all the links up to 100%. We would do this to avoid the possibility of a link becoming idle because an idle link hurts throughput. The problem with this strategy is that increasing the number of packets in the network also increases the length of the queues at each router. Such persistent queues mean packets are delayed in the network, or worse, dropped. Having to drop packets in the middle of the network not only impacts delay but also hurts throughput because upstream link bandwidth has been wasted on a packet that was not successfully delivered all the way to the destination.1
- 1
We sometimes use the term goodput instead of throughput to emphasize that we care about data that is successfully delivered through the network to the receiver, as opposed to just transmitted by the sender.
The ratio of throughput to delay is a general metric for evaluating the effectiveness of a resource allocation scheme. This ratio is sometimes referred to as the power of the system:
Intuitively, the objective is to maximize this ratio, which is a function of how much load you place on the system. The load, in turn, is set by the resource allocation mechanism. Figure 11 gives a representative power curve, where, ideally, the resource allocation mechanism would operate at the peak of this curve. To the left of the peak, the mechanism is being too conservative; that is, it is not allowing enough packets to be sent to keep the links busy. To the right of the peak, so many packets are being allowed into the network that either (a) increases in delay (denominator) due to queuing are starting to dominate any small gains in throughput, or (b) throughput (numerator) actually starts to drop due to packets being dropped.
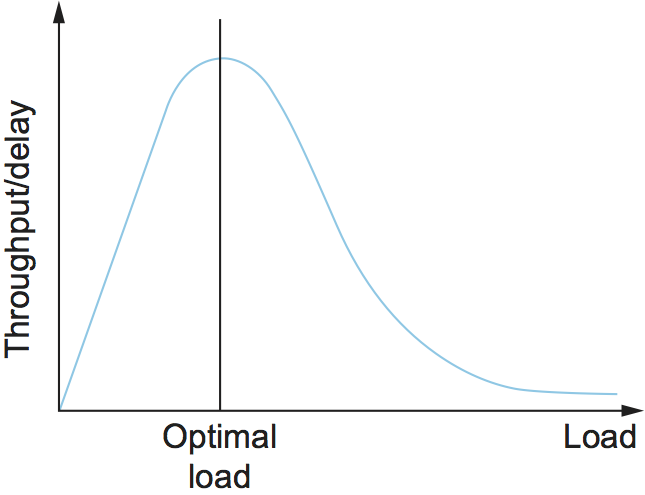
Figure 11. Ratio of throughput to delay as a function of load.
Moreover, we need to be concerned about what happens even when the system is operating under heavy load—towards the right end of the curve in Figure 11. Ideally, we would like to avoid the situation in which the system throughput approaches zero. The goal is for the mechanism to be stable—where packets continue to get through the network even when it is operating under heavy load. If a mechanism is not stable under heavy load, the network will suffer from congestion collapse.
Note that while both “persistent queues” and “congestion collapse” are to be avoided, there is no precise definition for the threshold at which a network suffers from either. They are both subjective judgments about an algorithm’s behavior, where at the end of the day, latency and throughput are the two performance indicators that matter.
3.2.2 Fairness
The effective utilization of network resources is not the only criterion for judging a resource allocation scheme. We must also consider the issue of fairness. However, we quickly get into murky waters when we try to define what exactly constitutes fair resource allocation. For example, a reservation-based resource allocation scheme provides an explicit way to create controlled unfairness. With such a scheme, we might use reservations to enable a video stream to receive 1 Mbps across some link while a file transfer receives only 10 kbps over the same link.
In the absence of explicit information to the contrary, when several flows share a particular link, we would like for each flow to receive an equal share of the bandwidth. This definition presumes that a fair share of bandwidth means an equal share of bandwidth. But, even in the absence of reservations, equal shares may not equate to fair shares. Should we also consider the length of the paths being compared? For example, as illustrated in Figure 12, what is fair when one four-hop flow is competing with three one-hop flows?
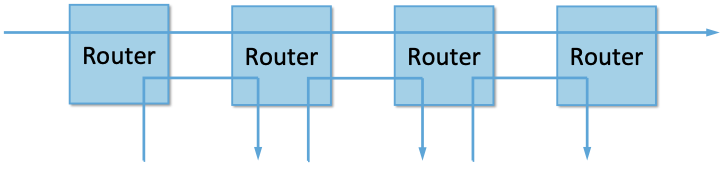
Figure 12. One four-hop flow competing with three one-hop flows.
Assuming that the most fair situation would be one in which all flows receive the same bandwidth, networking researcher Raj Jain proposed a metric that can be used to quantify the fairness of a congestion-control mechanism. Jain’s fairness index is defined as follows. Given a set of flow throughputs
(measured in consistent units such as bits/second), the following function assigns a fairness index to the flows:
The fairness index always results in a number between 0 and 1, with 1 representing greatest fairness. To understand the intuition behind this metric, consider the case where all n flows receive a throughput of 1 unit of data per second. We can see that the fairness index in this case is
Now, suppose one flow receives a throughput of \(1 + \Delta\). Now the fairness index is
Note that the denominator exceeds the numerator by \((n-1)\Delta^2\). Thus, whether the odd flow out was getting more or less than all the other flows (positive or negative \(\Delta\)), the fairness index has now dropped below one. Another simple case to consider is where only k of the n flows receive equal throughput, and the remaining n-k users receive zero throughput, in which case the fairness index drops to k/n.
Further Reading
R. Jain, D. Chiu, and W. Hawe. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems. DEC Research Report TR-301, 1984.
In the next section we revisit the notion of fairness as it applies to the deployment of new congestion control algorithms. As noted above, it is not as clear-cut as it might first appear.
TCP-friendly rate control (TFRC) also uses the notion of fairness. TFRC uses the TCP throughput equation (discussed in Section 1.3) to estimate the share of a congested link’s bandwidth that would be obtained by a flow that implemented TCP’s congestion control scheme, and sets that as a target rate for an application to send data. The application can then make decisions to help it hit that target rate. For example, a video streaming application might choose among a set of different encoding quality levels to try to maintain an average rate at the “fair” level as determined by TFRC.
3.3 Comparative Analysis
The first step in evaluating any congestion control mechanism is to measure its performance in isolation, including:
The average throughput (goodput) flows are able to achieve.
The average end-to-end delay flows experience.
That the mechanism avoid persistent queues across a range of operating scenarios.
That the mechanism be stable across a range of operating scenarios.
The degree to which flows receive a fair share of the available capacity.
The inevitable second step is to compare two or more mechanisms. This is because, given the decentralized nature of the Internet, there is no way to ensure uniform adoption of just one mechanism. Comparing quantitative metrics like throughput is easy. The problem is how to evaluate multiple mechanisms that might coexist, competing with each other for network resources.
The question is not whether a given mechanism treats all of its flows fairly, but whether mechanism A is fair to flows managed by mechanism B. If mechanism A is able to measure improved throughput over B, but it does so by being more aggressive, and hence, stealing bandwidth from B’s flows, then A’s improvement is not fairly gained and may be discounted. It should be evident that the Internet’s highly decentralized approach to congestion control works because a large number of flows respond in a cooperative way to congestion, which opens the door to more aggressive flows improving their performance at the expense of those which implement the accepted, less aggressive algorithms.
Further Reading
R. Ware, et al. Beyond Jain’s Fairness Index: Setting the Bar for the Deployment of Congestion Control Algorithms. ACM SIGCOMM HotNets. November 2019.
Arguments like this have been made many times over the last 30 years, which has raised a high bar to the deployment of new algorithms. Even if global deployment of a new algorithm would be a net positive, incremental deployment (which is the only real option) could negatively impact flows using existing algorithms, leading to a reluctance to deploy new approaches. But such analysis suffers from three problems, as identified by Ranysha Ware and colleagues:
Ideal-Driven Goalposting: A fairness-based threshold asserts new mechanism B should equally share the bottleneck link with currently deployed mechanism A. This goal is too idealistic in practice, especially when A is sometimes unfair to its own flows.
Throughput-Centricity: A fairness-based threshold focuses on how new mechanism B impacts a competitor flow using mechanism A by focusing on A’s achieved throughput. However, this ignores other important figures of merit for good performance, such as latency, flow completion time, or loss rate.
Assumption of Balance: Inter-mechanism interactions often have some bias, but a fairness metric cannot tell whether the outcome is biased for or against the status quo. It makes a difference in terms of deployability whether a new mechanism B takes a larger share of bandwidth than legacy mechanism A or leaves a larger share for A to consume: the former might elicit complaints from legacy users of A, where the latter would not. Jain’s Fairness Index assigns an equivalent score to both scenarios.
Instead of a simple calculation of Jain’s fairness index, Ware advocates for a threshold based on harm, as measured by a reduction in throughput or an increase in latency or jitter. Intuitively, if the amount of harm caused by flows using a new mechanism B on flows using existing mechanism A is within a bound derived from how much harm A-managed flows cause other A-managed flows, we can consider B deployable alongside A without harm. Ware goes on to propose concrete measures of acceptable harm, which turns out to be more complicated than it might first appear. Even with a single congestion control algorithm, the amount of harm that one flow causes another depends on factors such as its RTT, start time, and duration. Thus measures of harm need to take into account the range of impacts that different flows have on each other under the existing regime and aim to do no worse with a new algorithm.
3.4 Experimental Methodology
Our approach to evaluating congestion-control mechanisms is to measure their performance on real systems, and as we pointed out in Chapter 1, the de facto specification of the respective mechanisms is the version implemented in Linux. We now describe one specific way to perform those measurements, illustrating one methodology that is widely practiced today. Our approach uses Netesto (Network Test Toolkit), a collection of software tools available on GitHub. The alternative is simulation-based, with NS-3 being the most popular open source tool.
Note that while the experiments described in this section measure real congestion control algorithms (which, of course, we have not yet described in any detail), the intent is to outline how algorithms are evaluated, and not to actually draw any conclusions about specific mechanisms.
3.4.1 Experimental Setup
Our approach uses real TCP senders/receivers running on Linux hosts,
with a range of behaviors studied using a combination of kernel
packages like netem and tbf qdisc. Performance data is then
collected using tcpdump. The network connecting the end-hosts is
constructed from a combination of real switches and emulated elements,
supporting for example, wide-area delays and low-bandwidth links.
The experiments can be characterized along two orthogonal dimensions. One is the topology of the network. This includes link bandwidths, RTTs, buffer sizes, and so on. The other dimension is the traffic workload we run on the network. This includes the number and duration of flows, as well as the characteristics of each flow (e.g., stream vs. RPC).
With respect to network topology, we evaluate algorithms on three specific configurations:
LAN with \(20\mu\rm{s}\) RTT and 10-Gbps link bandwidth. This scenario represents servers in the same datacenter rack.
WAN with 10ms RTT and 10-Gbps link bandwidth, with delay introduced on the receiver by configuring a 20,000 packet send queue. The bottleneck is a real switch with shallow buffers (1-2 MB). This is a good scenario to visualize the algorithm’s dynamics when looking at two to three flows.
WAN with 40ms RTT and 10/100-Mbps bottleneck bandwidth, with an intermediate router introduced to reduce the link bandwidth to 10 or 100 Mbps. This scenario reflects a connection an end-user might experience on a modern network.
Figure 13 shows the topology for the first two
scenarios, where the senders and receivers are connected through a
single switch. Delay is achieved for the second scenario using
netem in the Receiver, which affects only the ACKs being sent
back.
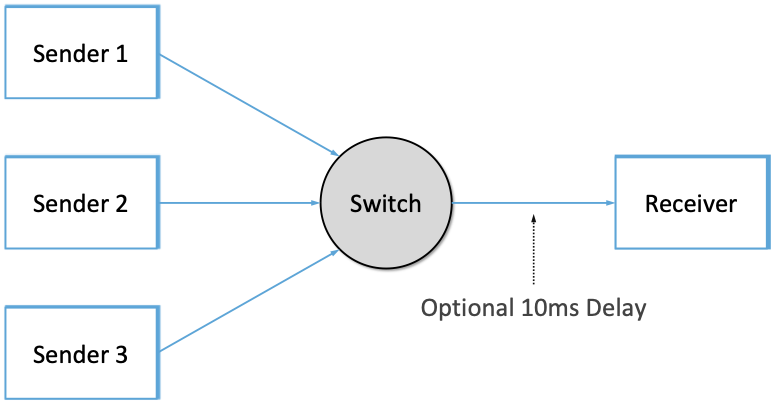
Figure 13. Topology for 10-Gbps Tests, optionally with 10ms of delay introduced.
Figure 14 shows the topology for the third
scenario, where the router is implemented by a server-based forwarder
that throttles outgoing link bandwidth using tbf qdisc.
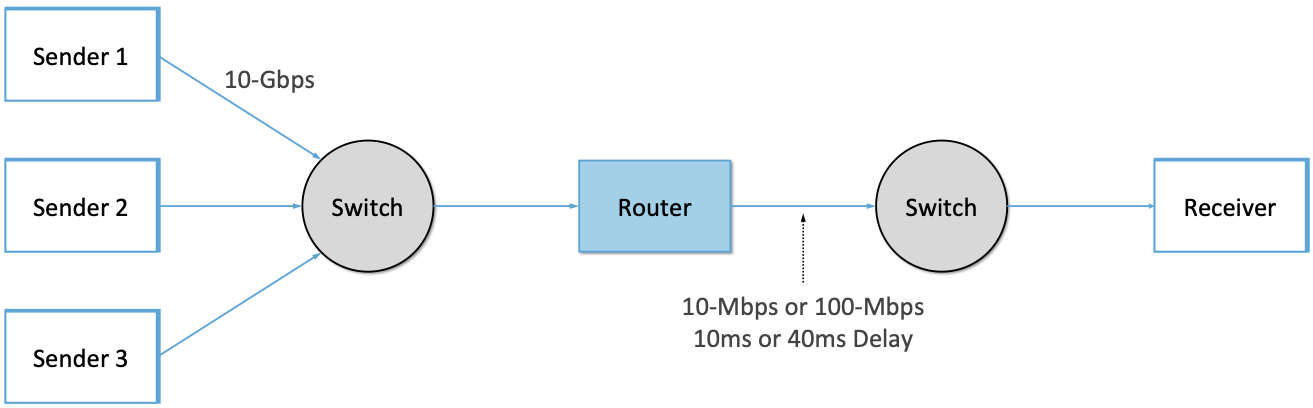
Figure 14. Topology for 10-Mbps and 100-Mbps Tests with 10ms or 40ms of delay introduced.
With respect to traffic workload, we evaluate the dynamics and fairness of algorithms with the following tests:
2-flow Test: The first flow lasts 60 seconds, and the second flow lasts 20 seconds and starts 22 seconds after the first one.
3-flow Test: The first flow lasts 60 seconds, the second flow lasts 40 seconds and starts 12 seconds after the first one, the third flow lasts 20 seconds and starts 26 seconds after the first one.
These tests make it possible to:
Examine how quickly existing flows adapt to new flows.
Examine how quickly flows adapt to released bandwidth from terminating flows.
Measure fairness between flows with the same (or different) congestion algorithm(s).
Measure levels of congestion.
Identify conditions under which performance changes abruptly, signalling a possible instability.
Additional tests include a combination of streaming, plus 10-KB and 1-MB RPCs. These tests allow us to see if the smaller RPC flows are penalized, and if so, by how much. These tests make it possible to:
Study behavior under increasing loads.
Measure the performance (throughput and latency) of 1-MB and 10-KB flows, as well as how fairly is the available bandwidth divided between them.
Identify conditions when the retransmissions or latency change abruptly, signalling an instability.
3.4.2 Example Results
The following shows some example results, selected to illustrate the evaluation process. We start with a simple 2-flow experiment, where both flows are managed by the same congestion-control algorithm. Figure 15 shows the resulting goodput graph. As one would hope, once the second flow (in red) starts just after 20 seconds, the goodput of both flows converge towards a nearly equal sharing of the available bandwidth. This convergence is not immediate (the two plots cross over roughly ten seconds after the second flow begins), a behavior other algorithms try to correct (e.g., by using explicit feedback from routers). On the plus side, the first flow does quickly adapt to the released bandwidth once the second flow terminates.

Figure 15. Goodput (bytes per second delivered end-to-end) realized by two flows running under the same congestion-control algorithm.
It is also possible to look more closely at these two flows, for example, by tracking the congestion window for each. The corresponding plot is shown in Figure 16. Not surprisingly, different algorithms would have different “patterns” to congestion windows over time, as we will see in the next chapter.
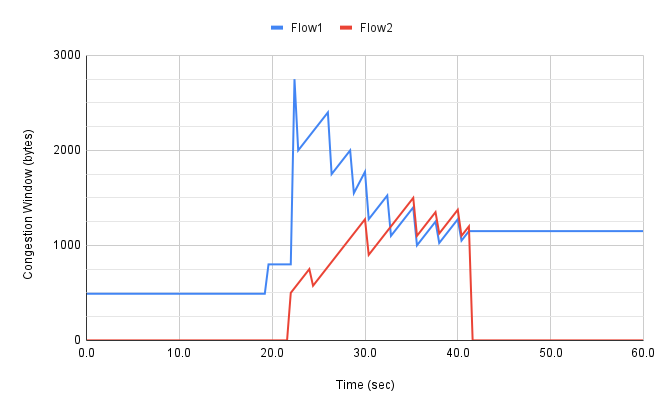
Figure 16. Congestion window (measured in bytes) for two flows competing for bandwidth under the same congestion-control algorithm.
We could repeat these experiments but vary the algorithm used by one of the flows. This would allow us to visualize how the two algorithms interact. If they are both fair, you would expect to see results similar to Figure 15. If not, you might see a graph similar to Figure 17, in which the second flow (Algorithm B) aggressively takes bandwidth away from the first flow (Algorithm A).
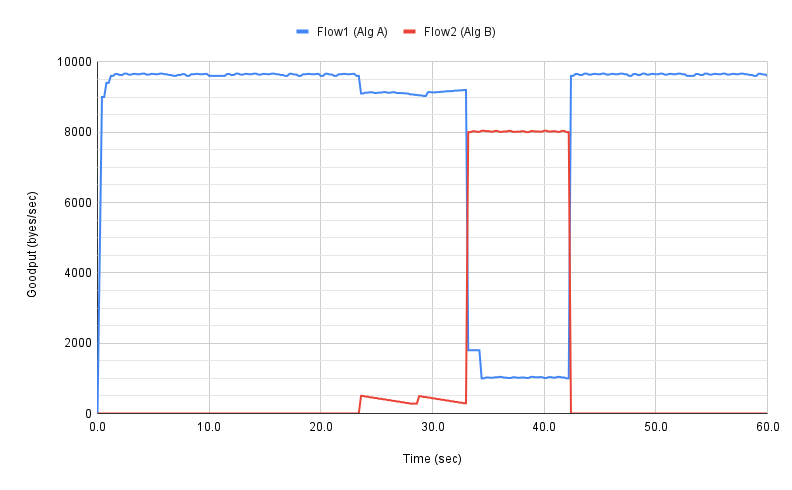
Figure 17. Goodput (bytes per second delivered end-to-end) realized by two flows running under different congestion-control algorithms, with one flow receiving significantly less bandwidth than the other.
These experiments can be repeated with three concurrent flows, but we turn next to evaluating how various algorithms treat different workloads. In particular, we are interested in the question of size fairness, that is, how a given algorithm treats back-to-back 10-KB or 1-MB RPC calls when they have to compete with ongoing stream-based flows. Some example results are shown in Figure 18 (1-MB RPCs) and Figure 19 (10-KB RPCs). The figures show the performance of five different algorithms (represented by different colors), across test runs with 1, 2, 4, 8, and 16 concurrent streaming flows.

Figure 18. Average goodput (measured in Gbps) realized by a sequence of 1-MB RPC calls for five different algorithms, when competing with a varied number of TCP streams.
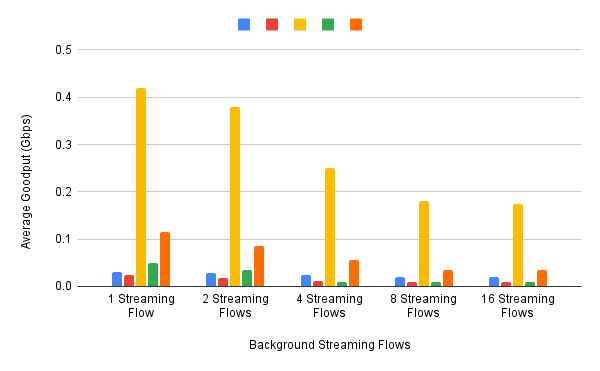
Figure 19. Average goodput (measured in Gbps) realized by a sequence of 10-KB RPC calls for five different algorithms, when competing with a varied number of TCP streams.
The 1-MB results are unsurprising, with no significant outliers across the five algorithms, and the average goodput decreasing as the RPCs compete with more and more streams. Although not shown in Figure 18, the fourth algorithm (green), which performs best when all flows are stream-based, suffers a significant number of retransmissions when sharing the available bandwidth among RPC calls.
The 10-KB results do have a significant outlier, with the third algorithm (yellow) performing significantly better; by a factor of 4x. If you plot latency rather than bandwidth—the more relevant metric for small-message RPC calls—it turns out the third algorithm both achieves the lowest latencies and does so consistently, with the 99th and 99.9-th percentiles being the same.
Finally, all of the preceding experiments can be repeated on a network topology that includes wide-area RTTs. Certainly inter-flow fairness and size fairness continue to be concerns, but there is also an increased likelihood that queuing delays become an issue. For example, Figure 20 shows the 99% latencies for four different algorithms when the network topology includes a 10-Mbps bottleneck link and a 40ms RTT. One important observation about this result is that the second algorithm (red) performs poorly when there is less than one bandwidth-delay product of buffering available at the bottleneck router, calling attention to another variable that can influence your results.
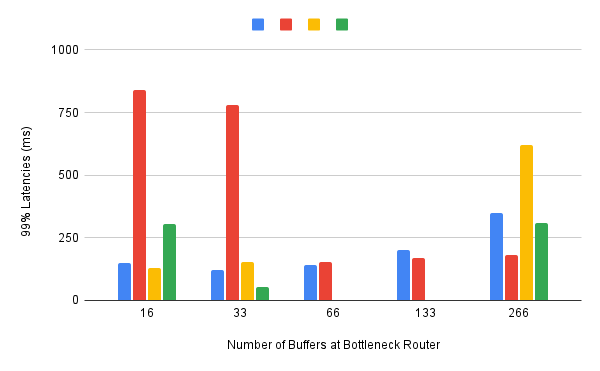
Figure 20. 99th percentile latencies for 10-KB RPC calls when competing with a single streaming flow on a 40ms WAN, measured for a different number of buffers at the bottleneck router.
We conclude this discussion of experimental methodology by permitting ourselves one summary evaluation statement. When looking across a set of algorithms and a range of topology/traffic scenarios, we conclude that: No single algorithm is better than all other algorithms under all conditions. One explanation, as these examples demonstrate, is how many factors there are to take into consideration. This also explains why congestion control continues to be a topic of interest for both network researchers and network practitioners.